Conditional Probability and Independence¶

In supervised machine learning, we are building predictive models that predict variance of some variable, using variance of some other variables. To model these connections, we have to learn Conditional Probabilities and Independence of events.

According to a survey, a person is happier if they are married. As a researcher, what is your take on it? You want to explore the effects of marriage on happiness. To study this, you collect the data as follows:

Id	Married	Happy
1	Yes	Yes
2	No	Yes
3	Yes	No
4	Yes	Yes
5	No	No

and so on...

1. Dependent Events :¶

Suppose the 100 such samples have following statistics

---	Happy Yes	Happy No	Total
Married Yes	42	28	70
Married No	6	24	30
Total	48	52	100

Let,

H be an event where a person chosen at random is 'Happy'
M be an event where a person chosen at random is 'Married'

\begin{align}P(H) = \frac{N(Happy)}{N(Sample\ Space)} = \frac{48}{100} =0.48 \end{align}\begin{align}P(M) = \frac{N(Married)}{N(Sample\ Space)} = \frac{70}{100} =0.70 \end{align}

Now, if we are already given that the person is married. Then what is the probability that the person is Happy?¶

Here we calculate the probability of the person being happy, given that he is married. That means, event M has already occured. We would search for occurence of event H in the sample space of M.

Thus, Conditional probability refers to the chances that some outcome occurs given that another event has also occurred. Mathematically,

\begin{align} P(A|B)=\ \frac{(A\ n\ B\ )}{B} \end{align}

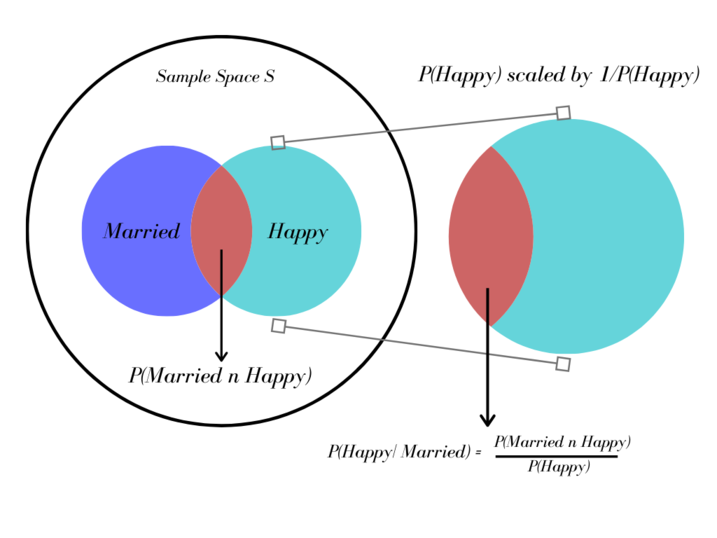
The total number of married people in the above dataset is : 70
The total people of married people who are happy is : 42

\begin{align} P(H|M)=\ \frac{42}{70}\ =\ 0.6 \end{align}\begin{align} P(H|M)\ >\ P(H) \end{align}

We can conclude that, the knowledge that the person is married helps us in better determining the probability of whether the person is happy. If the person is married, he/she is likely to be happy.

The events, H and M are said to be dependent events.¶

2. Independent Events :¶

Now, to demonstrate independent events consider, the 100 such samples with following statistics

---	Happy Yes	Happy No	Total
Married Yes	48	32	80
Married No	12	8	20
Total	60	40	100

Let,

H be an event where a person chosen at random is 'Happy'
M be an event where a person chosen at random is 'Married'

\begin{align}P(H) = \frac{N(Happy)}{N(Sample\ Space)} = \frac{60}{100} =0.60 \end{align}\begin{align}P(M) = \frac{N(Married)}{N(Sample\ Space)} = \frac{80}{100} =0.80 \end{align}

Now, we will calculate the probability P(H|M) - The probability of person being happy given that he is married.¶

The total number of married people in the above dataset is : 80
The total people of married people who are happy is : 48

\begin{align} P(H|M)=\ \frac{48}{80}\ =\ 0.6 \end{align}\begin{align} P(H|M)\ = \ P(H) \end{align}\begin{align} It\ can\ also\ be\ written\ as \end{align}\begin{align} P(H|M)\ =\ \frac{P(H\ n\ M)}{P(M)} \end{align}\begin{align} P(H\ n\ M)\ =\ P(H).\ P(M)\ \ \ \ \ (Since\ P(H|M)\ =\ P(H)) \end{align}

We can conclude that, the knowledge that the person is married gives no new information about the probability of whether the person is happy. Hence, we cannot determine whether the person is happy based on the knowledge of his marital status.

The events, H and M are said to be Independent events.¶

Let us demonstrate dependent and independent events with an example of 3 coin tossing.

In [2]:

from IPython.display import display
from IPython.display import HTML
display(HTML('<style>.prompt{width: 0px; min-width: 0px; visibility: collapse}</style>'))
display(HTML("<style>.container { width:100% !important; }</style>"))

from itertools import product

Defining a function to calculate probabilities¶

\begin{align} P(Event)\ =\ \frac{Number\ of\ Favourable\ Outcomes\ n(Event)}{Number\ of\ all\ possible\ outcomes\ n(Sample Space)} \end{align}

In [28]:

def calculate_probability(E,S):
    return(len(E)/len(S))

Sample Space¶

Generate Sample Space for 3 coin tossings

In [29]:

##let us set the number of coin tossings as 3
n=3

sample_space=set(product(['H','T'],repeat=n))

print("The sample space is : \n",sample_space)
print("The number of sample points is ",len(sample_space))

The sample space is : 
 {('H', 'T', 'H'), ('T', 'H', 'H'), ('H', 'T', 'T'), ('T', 'H', 'T'), ('H', 'H', 'H'), ('T', 'T', 'H'), ('H', 'H', 'T'), ('T', 'T', 'T')}
The number of sample points is  8

Define Events and Calculate their Probabilities¶

We Define 3 events as follows :

A - Event where the first coin tossing is Tail
B - Event where the total coin tossings is 2
C - Event where the second coin tossing is Head

In [31]:

# Let A be an event where the first coin tossing is Tail
A ={a for a in sample_space if a[0]=='T'}
print ("Event A :\n",A)
print("The probability of event A is : ",calculate_probability(A,sample_space))

Event A :
 {('T', 'H', 'H'), ('T', 'T', 'H'), ('T', 'T', 'T'), ('T', 'H', 'T')}
The probability of event A is :  0.5

In [32]:

# Let B be an event where the total coin tossings is 2
B ={b for b in sample_space if b.count('T')==2}
print ("Event B :\n",B)
print("The probability of event B is : ",calculate_probability(B,sample_space))

Event B :
 {('T', 'H', 'T'), ('T', 'T', 'H'), ('H', 'T', 'T')}
The probability of event B is :  0.375

In [33]:

#let C be an event where the second coin tossing is Head
C ={c for c in sample_space if c[1]=='H'}
print ("Event C :\n",C)
print("The probability of event C is : ",calculate_probability(C,sample_space))

Event C :
 {('T', 'H', 'H'), ('H', 'H', 'H'), ('H', 'H', 'T'), ('T', 'H', 'T')}
The probability of event C is :  0.5

Defining Function to Calculate Conditional Probabilities¶

In [34]:

def conditional_probability(A1,A2):
    return (len(A1 & A2)/len(A2))

In [40]:

def are_independent(A1,A2,S=sample_space):
    return (calculate_probability(A1 &A2,S)==calculate_probability(A1,S)*calculate_probability(A2,S))

Dependent Event¶

In [41]:

print ("The conditional probability of event B given that event A has already occured is : ",conditional_probability(B,A))

The conditional probability of event B given that event A has already occured is :  0.5

Here, it is evident that occurence of event A affects the probability for occurence of event B.
P(B|A) > P(B)
Hence these events are dependent events.

Lets us verify again

In [42]:

print(are_independent(A,B,S=sample_space))

False

Independent Event¶

In [43]:

print ("The conditional probability of event C given that event A has already occured is : ",conditional_probability(C,A))

The conditional probability of event C given that event A has already occured is :  0.5

Here, it is evident that occurence of event A gives no new information for probability of occurence of event C
P(C|A) = P(C)
Hence these events are independent events.